Introduction
Voici un paradoxe proposé par Joseph Louis François Bertrand (1822 – 1900), un mathématicien, économiste et historien des sciences français.
«On trace au hasard une corde dans un cercle. Quelle est la probabilité pour qu’elle soit plus grande que le côté du triangle équilatéral inscrit ?»
Joseph Bertrand, Calcul des probabilités, Gauthier-Villars, 1889, p. 4. [1]Voir sur le site de la Bibliothèque Nationale de France : https://gallica.bnf.fr/ark:/12148/bpt6k99602b/f64.image. Nous y lisons « plus petite que », ce qui est sans doute une erreur, car les … Continue reading
En sciences, afin de vérifier des hypothèses, nous pouvons réaliser des expériences, mais également recourir à des simulations sur ordinateur, en construisant une représentation ou modèle mathématique, qui nous donne des informations, lorsque les représentations sont bonnes, sur le monde réel. [2] Voir les articles « Modèle mathématique » https://fr.wikipedia.org/wiki/Mod%C3%A8le_math%C3%A9matique et « Modélisation » https://www.universalis.fr/encyclopedie/modelisation-mathematique/ .
Joseph Bertrand nous propose plusieurs hypothèses. Nous les modéliserons à l’aide du logiciel Scratch, nous comparerons les résultats obtenus, nous percevrons l’intérêt des représentations graphiques et nous explorerons d’explorer les possibilités du langage « Scratch». [3] Pour en savoir plus sur ce langage et son environnement de développement : https://scratch.mit.edu/ ..
1. Exploration des hypothèses :
Plusieurs pistes de modélisations sont possibles, selon le procédé envisagé pour réaliser la consigne « On trace par hasard une corde dans un cercle ». Joseph Bertrand en décrit trois :
«On peut dire : si l’une des extrémités de la corde est connue, ce renseignement ne change pas la probabilité; la symétrie du cercle ne permet d’y attacher aucune influence, favorable ou défavorable à l’arrivée de l’événement demandé.
L’une des extrémité de la corde étant connue, la direction doit être réglée par le hasard. Si l’on trace les deux côtés du triangle équilatéral ayant pour sommet le point donné, ils forment entre eux et avec la tangente trois angles de 60°. La corde, pour être plus grande que le côté du triangle équilatéral, doit se trouver dans celui des trois angles qui est compris entre les deux autres. La probabilité pour que le hasard entre trois angles égaux qui peuvent le recevoir le dirige dans celui-la semble, par définition, égale à.
On peut dire aussi : si l’on connait la direction de la corde, ce renseignement ne change pas la probabilité. La symétrie du cercle ne permet d’y attacher aucune influence, favorable ou défavorable à l’arrivée de l’événement demandé.
La direction de la corde étant donnée, elle doit, pour être plus grande que le côté du triangle équilatéral, couper l’un ou l’autre des rayons qui composent le diamètre perpendiculaire, dans la moitié la plus voisine du centre. La probabilité pour qu’il en soit ainsi semble, par définition, égale à.
On peut dire encore : choisir une corde au hasard, c’est en choisir au hasard le point milieu. Pour que la corde soit plus grande que le côté du triangle équilatéral, il faut et il suffit que le point milieu soit à une distance du centre plus petite que la moitié du rayon, c’est-à-dire à l’intérieur d’un cercle quatre fois plus petit en surface. Le nombre des points situés dans l’intérieur d’une surface quatre fois moindre est quatre fois moindre. La probabilité pour que la corde dont le milieu est choisi au hasard soit plus grande que le côté du triangle équilatéral semble, par définition, égale à.
Entre ces trois réponses, quelle est la véritable? Aucune des trois n’est fausse, aucune n’est exacte, la question est mal posée.»Ibidem, p. 5.
1.1. Première hypothèse : choisir deux points et tracer la corde
Nous plaçons un point ![]() n’importe où sur le cercle. Tous les points du cercle conviennent. Cela n’a aucun effet sur la probabilité, car tous les cas possibles sont favorables.
n’importe où sur le cercle. Tous les points du cercle conviennent. Cela n’a aucun effet sur la probabilité, car tous les cas possibles sont favorables.
Nous plaçons un deuxième point ![]() , et traçons le segment
, et traçons le segment ![]() .
.
Dans quel cas la corde obtenue est-elle plus longue que le côté du triangle équilatéral inscrit ?
Voir l’activité sur le site de GeoGeBra : https://www.geogebra.org/m/qebgd8w3
Nous traçons le triangle équilatéral ![]() et déplaçons le point
et déplaçons le point ![]() sur le cercle.
sur le cercle.
Tant que ![]() est sur le petit arc
est sur le petit arc ![]() , la corde
, la corde ![]() est plus grande qu’un côté du triangle équilatéral.
est plus grande qu’un côté du triangle équilatéral.
Lorsque ![]() est sur le grand arc
est sur le grand arc ![]() , la corde
, la corde ![]() est plus petite.
est plus petite.
Nous pouvons dire : les sommets du triangle équilatéral partagent le cercle en trois parties égales. Les cas favorables pour le point ![]() se trouvent sur une de ces parties, soit l’arc
se trouvent sur une de ces parties, soit l’arc ![]() ou
ou ![]() du cercle. Les points possibles sont tous les points du cercle.
du cercle. Les points possibles sont tous les points du cercle.
Nous pouvons aussi dire : la corde ![]() peut pivoter autour du point
peut pivoter autour du point ![]() sur 180°. Lorsqu’elle parcourt l’angle
sur 180°. Lorsqu’elle parcourt l’angle ![]() , elle est plus longue qu’un côté du triangle équilatéral. Elle est plus courte lorsqu’elle parcourt les angles
, elle est plus longue qu’un côté du triangle équilatéral. Elle est plus courte lorsqu’elle parcourt les angles ![]() et
et ![]() . Nous savons que :
. Nous savons que : ![]() .
.
Donc, la probabilité pour qu’une corde tracée au hasard soit plus grande que le côté du triangle équilatéral inscrit est :
![]()
1.2. Deuxième hypothèse : choisir un point sur un rayon et tracer la perpendiculaire à ce rayon
2. Modélisations
2.1. Choisir deux points sur le cercle par les abscisses
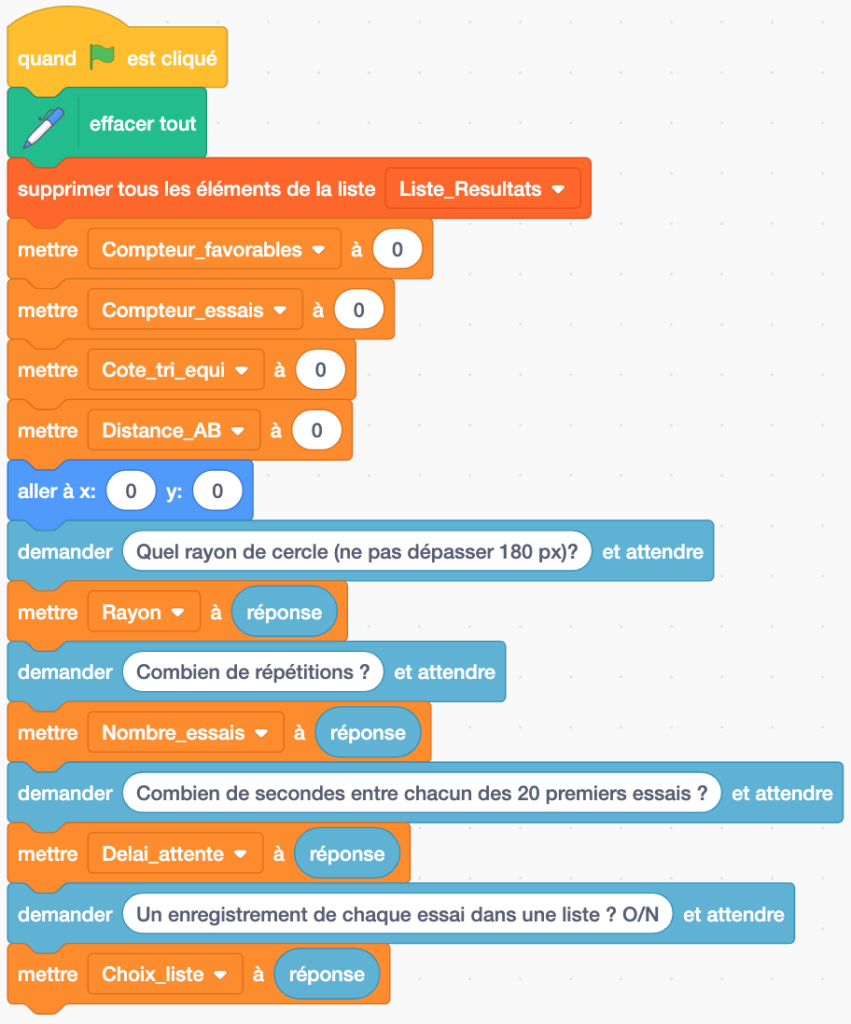
L’initialisation commence par les remises à 0 de :
– La liste des résultats (coordonnées de A, de B, longueur de la corde AB) qui permet d’exporter les valeurs dans un fichier texte *.txt et de l’ouvrir dans un tableur,
– le compteur de cas favorables,
– le compteur de cas testés,
– la longueur du côté du triangle équilatéral inscrit,
– la longueur des cordes AB
Ensuite, le programme demande de préciser :
– le rayon du cercle,
– le nombre de répétitions à réaliser,
– la temporisation à respecter entre les vingt premières itérations, afin de visualiser le fonctionnement du programme,
– la demande d’enregistrer chaque essai dans une liste.
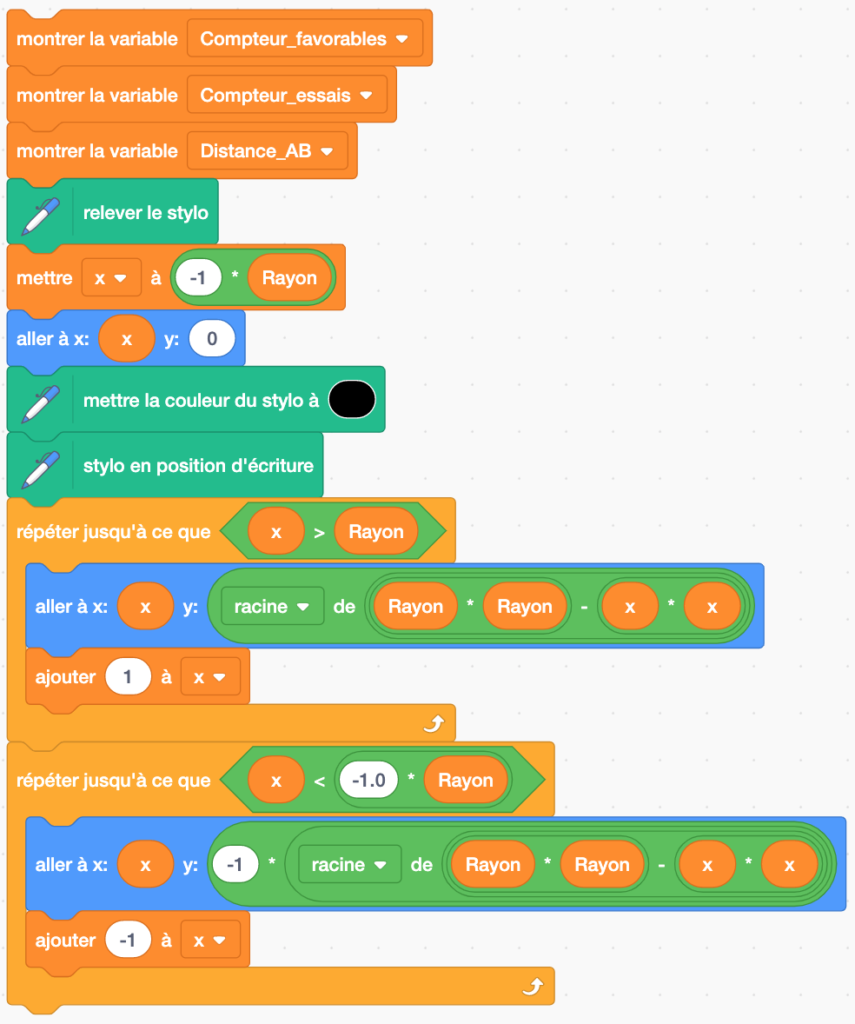
Ensuite, le programme :
– affiche les compteurs des essais, des cas favorables, et la longueur de chaque corde trace le cercle,
– trace le cercle, d’abord le demi-cercle supérieur, puis le demi-cercle inférieur.
Pour cela, pour chaque valeur entière de l’abscisse ![]() comprise entre l’opposé du
comprise entre l’opposé du ![]() et le
et le ![]() , il calcule l’ordonnée positive du point et trace le déplacement jusqu’à ce point en noir.
, il calcule l’ordonnée positive du point et trace le déplacement jusqu’à ce point en noir.
Puis, pour chaque valeur de l’abscisse comprise entre le ![]() et son opposé, il calcule l’ordonnée négative du point et trace également le déplacement en noir.
et son opposé, il calcule l’ordonnée négative du point et trace également le déplacement en noir.
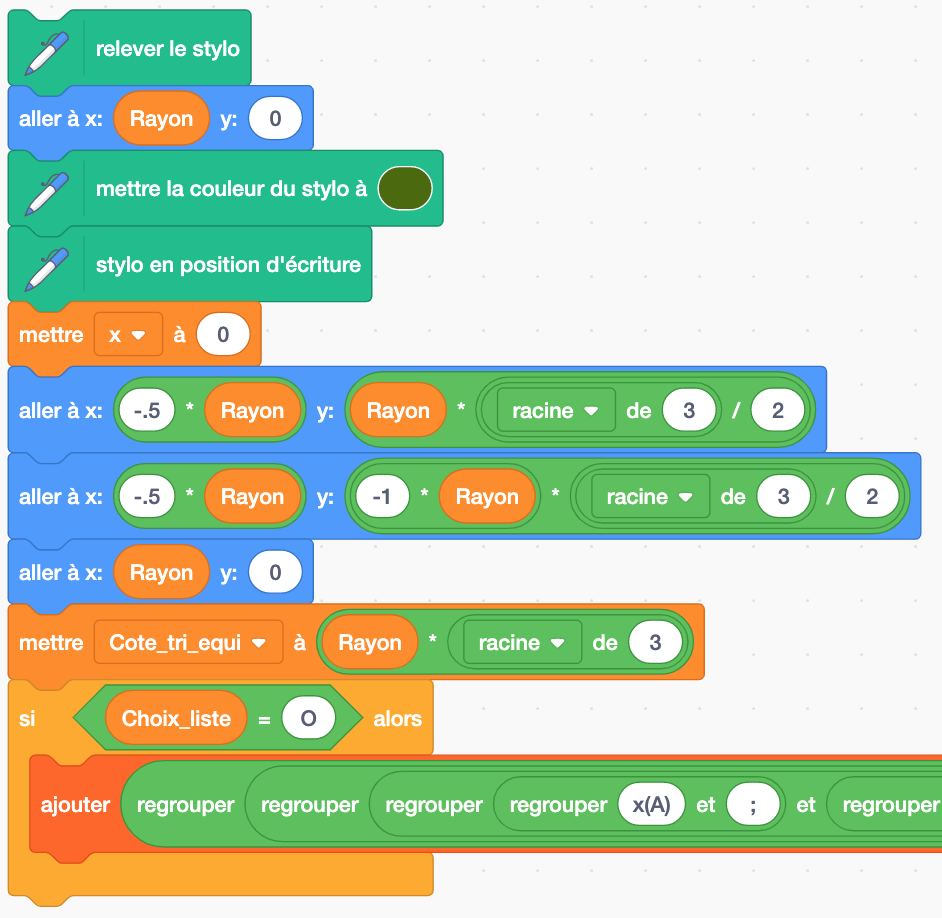
Le programme :
– trace le triangle équilatéral inscrit,
il part du point ![]() ,
,
va au point ![]() ,
,
puis au point ![]() ,
,
et revient au point ![]() ,
,
en appliquant le théorème de Pythagore.
– calcule la longueur d’un côté du triangle inscrit ![]() qu’il met dans la variable
qu’il met dans la variable ![]() , également en appliquant le théorème de Pythagore.
, également en appliquant le théorème de Pythagore.
– si l’enregistrement dans une liste a été demandé, il met dans la première ligne de la liste ![]() le texte des entêtes des colonnes afin de faciliter sa lecture par un tableur : les coordonnées de points
le texte des entêtes des colonnes afin de faciliter sa lecture par un tableur : les coordonnées de points ![]() et
et ![]() et la distance de
et la distance de ![]() à
à ![]() , séparées par un « ; », soit
, séparées par un « ; », soit
« ![]() »
»
On peut coder plus simplement :
« ![]() »
»
en évitant d’utiliser le code «regrouper» plusieurs fois, mais en fin de programme, il faudra bien l’utiliser pour mélanger variables et « ; » et alors, nous pourrons copier/coller !
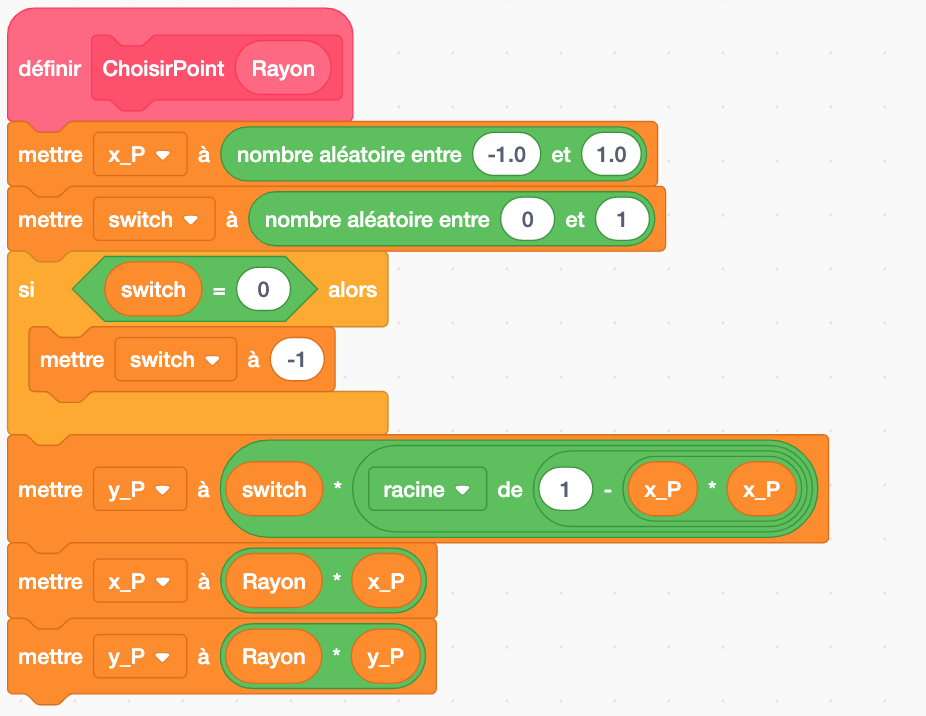
Pour choisir un point de façon aléatoire, nous définissons un bloc qui :
– choisit un nombre aléatoire entre -1.0 et 1.0, le point décimal suivi de 0 indique à Scratch que nous voulons des nombres décimaux et pas des entiers. Multiplié par le ![]() , nous obtenons une abscisse aléatoire.
, nous obtenons une abscisse aléatoire.
– choisit un nombre aléatoire entre 0 et 1. Comme ce sont des entiers, nous obtiendrons 0 ou 1, rien d’autre. Cela détermine si l’ordonnée sera positive ou négative.
– change le 0 en -1, afin d’obtenir une ordonnée négative par un simple produit,
– calcule l’ordonnée du point en appliquant le théorème de Pythagore. Selon la valeur de ![]() , elle sera positive ou négative.
, elle sera positive ou négative.
– calcule l’abscisse et l’ordonnée du point selon la valeur de ![]() .
.
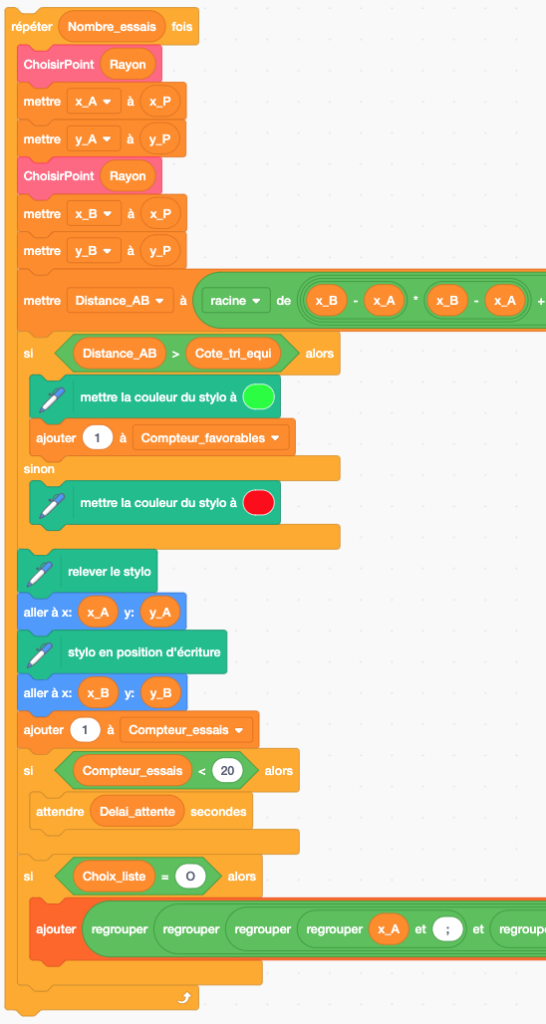
Voici la boucle qui simule la répétition des essais demandés selon la valeur de ![]() :
:
– choix du point ![]() ,
,
– choix du point ![]() ,
,
– calcul de la longueur de la corde ![]() en utilisant le théorème de Pythagore,
en utilisant le théorème de Pythagore,
– si cette longueur est plus grande que celle du côté du triangle équilatéral inscrit, incrémentation du compteur d’essai réussi ![]() d’une unité et mise au vert de la couleur du stylo, sinon mise au rouge,
d’une unité et mise au vert de la couleur du stylo, sinon mise au rouge,
– tracé de la corde ![]() ,
,
– incrémentation du compteur ![]() ,
,
– délai d’attente si demandé au début,
– inscription de l’essai dans la liste ![]() , par
, par
« ![]() »
»
en regroupant les éléments 2 par 2
La liste ![]() peut être exportée sous forme de fichier texte. A l’ouverture par un tableur, les « ; » seront reconnus comme séparateurs de cellules.
peut être exportée sous forme de fichier texte. A l’ouverture par un tableur, les « ; » seront reconnus comme séparateurs de cellules.
Cela permet d’utiliser les valeurs collectées durant la simulation.

A la fin, le programme montre les différents résultats de la simulation :
– nombre d’essais réalisés,
– nombre de cas favorables trouvés,
– dernière longueur ![]() trouvée,
trouvée,
– éventuellement la liste des essais. Un clic droit sur la liste permet de l’exporter.
2.2. Choisir deux points sur le cercle par les angles au centre
Notes
| ↑1 | Voir sur le site de la Bibliothèque Nationale de France : https://gallica.bnf.fr/ark:/12148/bpt6k99602b/f64.image. Nous y lisons « plus petite que », ce qui est sans doute une erreur, car les propositions de l’auteur qui suivent se réfèrent au cas d’une corde « plus grande que ». |
|---|---|
| ↑2 | Voir les articles « Modèle mathématique » https://fr.wikipedia.org/wiki/Mod%C3%A8le_math%C3%A9matique et « Modélisation » https://www.universalis.fr/encyclopedie/modelisation-mathematique/ . |
| ↑3 | Pour en savoir plus sur ce langage et son environnement de développement : https://scratch.mit.edu/ . |
