Une question

Janvier 2021.
Un samedi soir, durant l’émission OEED de France 2, apparaît ce tableau, diffusé sur Internet par un certain «Mika Denissot».
Surpris, intrigué, je me pose une question : comment l’auteur a-t-il construit ce tableau, manifestement dans le but de rassurer ?
C’est quoi cette image ?
D’abord, comment l’image est-elle construite ?
Le titre « Voici les survivants au COVID-19 » nous saisit par notre désir : nous désirons évidemment être parmi les survivants.
Ensuite, une liste de sept pays avec des pourcentages très précis : au millième de % près! Suit une suggestion à « changer de point de vue » et un point d’interrogation.
L’auteur nous suggère donc de regarder non plus les décès, mais les survivants. Il suggère qu’au moins 99,9 % des humains, des habitants de la terre, survivront. De plus, moins de 0,1 % de décès, ce ne semble pas être beaucoup …
Et nous glissons doucement dans le déni, dire que non, que ce n’est pas grave, on en fait trop avec ce virus, «Hakuna matata», pas de souci, vivons notre vie …
C’est notre désir, c’est notre rêve, … mais n’est-ce pas une illusion, à laquelle nous voudrions croire ?
Regardons de plus près.
D’où sortent ces chiffres ?
D’où viennent les pourcentages ? Ce n’est pas précisé, mais nous supposons qu’ils sont le fruit d’un passage du «verre à moitié vide» au «verre à moitié plein», le résultat d’une simple soustraction à partir de la mortalité :
![]()
Par exemple, pour la Belgique :
![]()
L’auteur se baserait sur une mortalité de
Est-ce logique ?
Est-ce exact ?
Deuxième question : malgré cela, ces statistiques sont-elles exactes ?
Une mortalité de ![]() pour la Belgique ? Vérifions en effectuant le calcul à l’envers, même si le résultat sera approximatif :
pour la Belgique ? Vérifions en effectuant le calcul à l’envers, même si le résultat sera approximatif :
Au 31 décembre 2020, la Belgique comptait ![]() habitants,
habitants,
[2]Site de Statbel : https ://statbel.fgov.be/fr/themes/population/structure-de-la-population donc:
![]()
Cette valeur était atteinte … vers le 21 avril 2020 !
Et en France métropolitaine ? Elle comptait
![]()
Ce nombre était atteint … vers le 29 avril 2020 !
Donc, ce tableau a été peut-être exact, … à la fin du mois d’avril 2020 [4]Selon les statistiques du site de l’OMS : https://covid19.who.int .
Et nous ne savons que trop que la pandémie s’est poursuivie, avec ses comptages des contaminations, des hospitalisations, des décès, et heureusement des guérisons et des vaccinations.
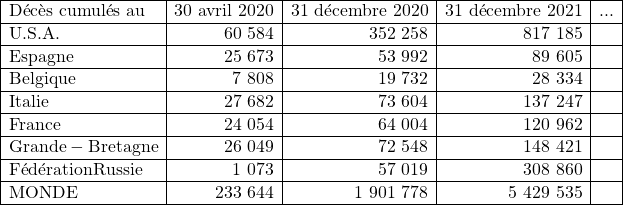
Nombres des décès cumulés – Source : Site O.M.S. – 18 janvier 2022
À partir de cet exemple, nous pouvons déterminer des critères qui permet d’accorder confiance à des statistiques, … ou pas : l’article précise-t-il quand et par qui les données ont été rassemblées ? Et où ? comment ? avec quelles quelles motivations ? dans quel but ? Les marges d’erreur des estimations sont-elles mentionnées ? etc.
Un monde réduit …
Regardons aussi les pays mentionnés : Etats-Unis, Espagne, Belgique, Italie, France, Royaume-Uni, Russie. Sept pays d’Europe, sauf un, et sept pays, sauf un, classés par les Nations Unies en fonction de l’«indice de développement humain» comme d’indice «très élevé» et, sauf pour la Russie, «en augmentation». [5] https://fr.wikipedia.org/wiki/Liste_des_pays_par_IDH#IDH_2015_(publié_en_2016)[6]
Nous ne devons donc pas nous attendre à de grands écarts, puisque ce sont des pays de niveaux comparables concernant la santé, l’éducation et l’économie.
Mais c’est une pandémie, qui concerne tous les pays du monde, quel que soit leur «indice de développement humain», alors pourquoi ce choix ?
De plus, nous verrons plus loin que, lorsqu’une étude rencontre des écarts statistiques importants, elle devient fructueuse car elle conduit à poser des questions, émettre des hypothèses, chercher des réponses, faire avancer les recherches.
Déjà dans le tableau au début de notre article, nous pouvons constater qu’il y avait plus de décès en Belgique. Pourquoi ? Rapidement, il a été signalé que certains Etats ne prenaient en compte que les décès survenus à l’hôpital, et que d’autres, comme la Belgique, y liaient des décès survenus en maisons de repos et de soins.
La mortalité, c’est quoi ?
L’auteur n’a pas réellement changé de point de vue : passant du verre «à moitié plein» au verre «à moitié vide», il continue de regarder la mortalité !
Nous savons que la mortalité est un pourcentage qui rapporte le nombre de personnes décédées à l’ensemble de la population d’un pays.
Elle est utilisée principalement afin de comparer et de piloter les politiques de la santé. Elle n’est qu’un des éléments qui permettent d’évaluer la gravité d’une maladie.
Mais numériquement, elle rapporte le plus petit nombre disponible dans les statistiques, le nombre de décès au plus grand nombre disponible, c’est à dire le nombre total d’habitants du pays. En exprimé en %, elle apparaît après la virgule. On ne peut pas trouver plus petit.
Par contre, c’est LE risque majeur, celui que nous redoutons, que nous préférons ignorer, mais que nous rencontrerons inévitablement un jour : le point final de notre histoire personnelle sur la Terre. C’est notre seule vraie certitude.
Le pourcentage de mortalité est donc la statistique la plus rassurante : il n’y a que … ! Cela dépend de la variable à laquelle on rapporte le nombre de décès : population, nombre de malades, nombre d’hospitalisés, … ? La prudence s’impose.
Parler en nombres absolus de milliers ou de millions de décès comme le fait le site de l’OMS est plus réaliste, même si c’est plus inquiétant, et pourtant c’est la même variable : le nombre de décès.
D’autres outils que les pourcentages ?
Nous avons vu que le recours au «pourcentage» doit se faire avec prudence, car il peut minimiser l’importance de rapports entre deux grandeurs.
Remarquons que le site de l’OMS [6]Voir le site de l’OMS : https://covid19.who.int privilégie l’affichage des nombres bruts : nouveaux cas, cas confirmés, décès, et maintenant nombre de vaccins administrés. C’est en effet plus sûr.
D’autres outils statistiques nous permettent de nous faire des images plus réalistes d’un phénomène dans une population, car rapporter à 100 induit l’idée d’un petit village :
– rapporter le nombre de décès à 100 000 habitants, donc à des communes comme Namur (111 127 habitants), Leuven (102 126 h), Molenbeek (97 365 h), Mons (95 568 h), ou en France, Roubaix (98 089 h), Nancy (104 885 h), Caen (105 512 h).
– rapporter le nombre de décès à 1 000 000 habitants, donc à des villes comme Bruxelles-Capitale (1 200 322 h) , ou en France, Marseille (870 731 h) [7]Sources : Les articles https://fr.wikipedia.org/wiki/Liste_des_communes_de_Belgique_par_population et https://fr.wikipedia.org/wiki/Liste_des_communes_de_France_les_plus_peuplées .
Décès cumulés au 18 janvier 2022 :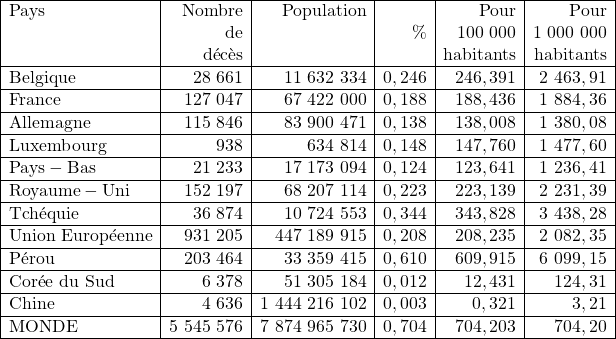
Nombre de décès cumulés – Source : Wikipedia – 18 janvier 2022 [8]A l’adresse : https://fr.wikipedia.org/wiki/Pand%C3%A9mie_de_Covid-19_par_pays_et_territoire consulté le 18 janvier 2022, attention, le site prévient : Le tableau du détail des cas par … Continue reading
Cela prend plus de sens, par exemple, si on peut dire : en Tchéquie, c’est comme si dans la ville de Namur, il y avait eu 7 décès par semaine pendant un an ou en Corée du Sud, 1 décès par mois pendant un an dans Mons.
Cela suggère aussi un vaste ensemble de questions, puisque certains pays s’en sortent nettement moins bien que d’autres : quel est l’état de leur système sanitaire ? leur population est-elle majoritairement jeune ou âgée ? quelles politiques habituelles de prévention sont pratiquées dans les épidémies ? comment déclarent-ils les décès ? …
Comparer des mortalités ?
Maintenant, comparons la mortalité due à la Covid-19 à d’autres grandeurs plus comparable, à d’autres mortalités. Voici un tableau présentant les trois causes de décès les plus importantes par année. Sur le site de Statbel, il manque encore quelques statistiques pour les dernières années.
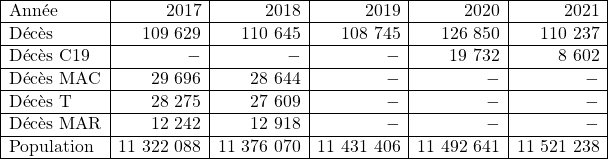
C19 = Covid-19
MAC = Maladies de l’appareil circulatoire
T = Tumeurs
MAR = Maladies de l’appareil respiratoire
Mortalité en Belgique – Sources : Statbel et OMS – 18 janvier 2022
En calculant les pourcentages correspondants par rapport au nombre de décès :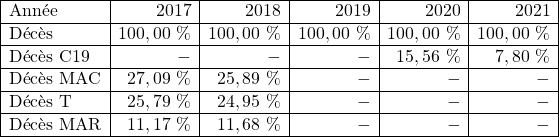
Une première constatation : alors que la mortalité «habituelle» tourne autour de 108 000 / 110 000 décès par an, il y a eu environ 17 000 décès de plus en 2020, ce qui est cohérent avec les 19 000 décès dus au Covid-19, car parmi ceux-ci, on peut comprendre qu’il y a des personnes qui seraient décédées d’autres maladies en 2020 s’il n’y avait pas eu l’épidémie.
Une deuxième constatation : pour l’année 2020, la maladie Covid-19 à elle seule prendrait la troisième place derrière le groupe de toutes les maladies de l’appareil circulatoire et le groupe de toutes les tumeurs et cancers. Ou bien si l’on inclut la Covid-19 dans le groupe des maladies de l’appareil respiratoire, celui-ci prendrait la première place !
Une troisième constatation : nous avons besoin de statistiques plus précises par maladies plutôt que par groupes de maladies. Le site es statistiques officielles sont parfois en retard mais
sachant que
Une étude statistique sérieuse ne peut se contenter d’un pourcentage, comparant deux variables. Au mieux, c’est une corrélation à étudier. Le travail commence avec trois, quatre variables et plus.
Dans notre cas, il y a d’autres indicateurs à utiliser afin de pouvoir dire si une situation est grave ou pas.
A côté de la mortalité, un autre indicateurCherchons à rémon l’intérêt augmente lorsque l’on ne compare plus deux variables, ce qui fournit qu’une corrélation, mais bien trois, quatre variables ou plus. Cherchons une réponse à la question : 0,17% de décès, est-ce grave ?
Comparons avec une autre statistique, la «mortalité générale» : combien de personnes meurent chaque année ?

Mortalité en Belgique – Sources : Statbel et OMS – 18 janvier 2022
Donc la Covid19 aura sans doute causé ![]() des décès de l’année.
des décès de l’année.
Nous pouvons être plus précis :
En Belgique, nous comptabilisons pour l’année 2020, 127 134 décès. [9]Sur le site de Statbel : https://statbel.fgov.be/fr/themes/population/mortalite-et-esperance-de-vie/mortalite-generale
Et le site de l’OMS affiche ![]() décès dûs à la Covid. La surmortalité de 16\ 500 décès est compatible avec les
décès dûs à la Covid. La surmortalité de 16\ 500 décès est compatible avec les ![]() décès dûs à la Covid-19.
décès dûs à la Covid-19.
Donc nous pouvons écrire :
![]()
soit :
![]()
Notes
